Q:)
Jika, rumus fungsi f(x) = 12x + 7x maka nilai yg tepat f(9) adalah
a). f(9) = 164
b). f(9) = 6.840
c). f(9) = 171
≈ Sertakan cara penyelesaian!
≈ ngasal → report!
≈ Rapi!
≈ Salah → koreksi!
≈ grade 3/5 dijamin beA!
)’
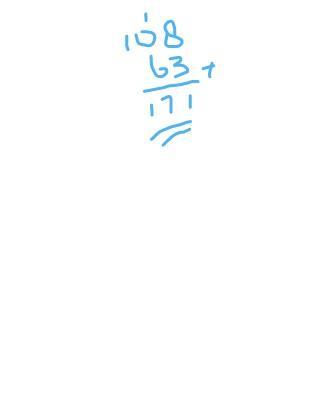
Mapel Matematika, Jenjang Sekolah Menengah Pertama
Penjelasan dengan langkah-langkah:
f(x) = 12x + 7x
f(9) = 12(9) + 7(9)
f(9) = (12 × 9) + (7 × 9)
f(9) = 108 + 63
f(9) = 171 (C)
Jawaban:
rumus fungsi:
- f(x) = 12x + 7x
- f(x) = 19x
maka nilai untuk f(9) adalah?
penyelesaian:
- f(x) = 12x + 7x
- f(x) = 19x
- f(9) = 19(9)
- f(9) = 19 × 9
- f(9) = 171
nilai yang tepat untuk f(9) adalah [c. f(9) = 171]
Pertanyaan Baru di Matematika
Rovie berangkat ke kota z pukul 15.35 mengendarai sepeda motor, dengankecepatan rata-rata 32 km/30 menit. jarak perjalanan yang harus ia tempuh adalah 80 km. jika rovi tiba di kota z pukul 17.15. berapa menitkah rovie berhenti di jalan untuk istirahat?
Matematika, Sekolah Menengah Pertama
Waktu Tempuh Dengan Motor :
t1 = s ÷ v
t1 = 80 ÷ 32/30
t1 = 80 × 30/32
t1 = 2.400/32
t1 = 75 Menit
t1 = 1 Jam 15 Menit
Waktu Tempuh Ke Kota z :
t2 = Waktu Berangkat – Waktu Sampai
t2 = 17.15 – 15.35
t2 = 1 Jam 40 Menit
Waktu Istirahat :
t3 = t2 – t1
t3 = 1 Jam 40 Menit – 1 Jam 15 Menit
t3 = 40 Menit – 15 Menit
t3 = 25 Menit
🙂
Penjelasan dengan langkah-langkah:
___________________________
Waktu tempuh ke kota z :
- Waktu Berangkat – Waktu Sampai
- = 17.15 – 15.35
- = 1 Jam 40 Menit
___________________________
Waktu Istirahat :
- Jam 40 Menit – 1 Jam 15 Menit
- = 40 Menit – 15 Menit
- = 25 Menit
___________________________
Kesimpulannya :
Jadi, berapa menitkah rovie berhenti di jalan untuk istirahat 25 menit mereka istirahat.
___________________________
#BelajarBersamaBrainly
Tentukan penyelesaian dari 12-5a>3a
Matematika, Sekolah Menengah Atas
12 – 5a > 3a
12 > 3a + 5a
12 > 8a
8a < 12
a < 12/8
a < 3/2
Jadi, penyelesaian dari 12-5a>3a adalah a<³/₂
Hasil dari 1255^0 + 556 =
Matematika, Sekolah Menengah Atas
Perpangkatan
Penjelasan dengan langkah-langkah:
- Nb : Semua Yang Dipangkatkan 0 Hasilnya Tetap 1
Penjelasan dengan langkah-langkah:
- 1255^0 + 556
- 1 + 556
- 557
- bilangan apa saja yang dipangkatkan dengan 0 maka hasilnya adalah 1
⅛ x 0,25 : 0,75 =
Janganngasal
Matematika, Sekolah Menengah Atas
Jawaban:
3/128
Penjelasan dengan langkah-langkah:
Jawaban:
1/24
Penjelasan dengan langkah-langkah:
1/8 × 0,25 : 0,75
= 1/8 × 25/100 : 75/100
=1/8 × 25/100 × 100/75
=1/8 × 1/4 × 4/3
=1/32 × 4/3
=4/96
=1/24
jika ada yg bingung bisa ditanyakan.
terimakasih semoga membantu ..
Q:) 
1). Lim 2x + x × 2x ÷ x || x → 5

2). 2x + x – 2 = 22 || x?

3). f(y) = y² + y || f(8) = …?
≈ Sertakan cara penyelesaian!
≈ ngasal → report!
≈ Rapi!
≈ Salah → koreksi!
≈ kalo bisa grade 3/5 dijamin beA!
Matematika, Sekolah Menengah Pertama
#1
Lim 2x + x × 2x ÷ x
x → 5
2(5) + 5 × 2(5) ÷ 5
= 10 + 5 × 10 ÷ 5
= 10 + 50 ÷ 5
= 10 + 10
= 20
#2
2x + x – 2 = 22
3x – 2 = 22
3x = 22 + 22
3x = 24
x = 24/3
x = 8
#3
f(y) = y² + y
f(8) = 8² + 8
f(8) = 8(8) + 8
f(8) = 64 + 8
f(8) = 72
🙂
« Penyelesaian Soal »
[ Soal ]
1). Lim 2x + x × 2x ÷ x || x → 5
2). 2x + x – 2 = 22 || x?
3). f(y) = y² + y || f(8) = …?
________________
✨ Penyelesaian
✨ Soal 1
- Diketahui
Lim 2x + x × 2x ÷ x
- Ditanya
Jika x → 5 ?
- Dijawab
x → 5
- Lim 2x + x × 2x ÷ x
- Lim 2(5) + 5 × 2(5) ÷ 5
- Lim ( 2 × 5 ) + 5 × ( 2 × 5 ) ÷ 5
- Lim ( 10 ) + ( 5 × 10 ) ÷ 5 )
- Lim ( 10 ) + ( 50 ÷ 5 )
- Lim 10 + 10
- Lim → 20 ☑
✨ Soal 2
- Diketahui
2x + x – 2 = 22
( Terdapat 2 Nilai x pada Pernyataan )
- Ditanya
x = ?
- Dijawab
- 2x + x – 2 = 22
- 3x = 22 + 2
- 3x = 24
- x = 24 ÷ 3
- x = 8 ☑
☞ Pembuktian
x = 8
- 2x + x – 2 = 22
- 2(8) + 8 – 2 = 22
- ( 2 × 8 ) + 8 – 2 = 22
- ( 16 + 8 ) – 2 = 22
- 24 – 2 = 22
- 22 ←→ 22 ( Terbukti ) ☑
✨ Soal 3
- Diketahui
f(y) = y² + y
- Ditanya
f(8) = …?
- Dijawab
- f(y) = y² + y
- f(8) = y² + y
- f(8) = 8² + y
- f(8) = ( 8 × 8 ) + 8
- f(8) = 64 + 8
- f(8) = 72 ☑
Kesimpulan ☚
- Maka, Hasil dari Lim 2x + x × 2x ÷ x Jika x → 5 adalah 20 ☑
- Maka, Nilai Dari x adalah 8 ☑
- Maka, Nilai Dari f(8) = 72 ☑
Semoga membantu–!
 Desain Grafis Indonesia Kumpulan Berita dan Informasi dari berbagai sumber yang terpercaya
Desain Grafis Indonesia Kumpulan Berita dan Informasi dari berbagai sumber yang terpercaya


