Desain Grafis Indonesia Kumpulan Berita dan Informasi dari berbagai sumber yang terpercaya
sebuah sampel terdiri dari atas 100 kendaraan bermotor masing masing telah dipilih dari populasi kendaraan bermotor yang ada di Bandung dan di Surabaya. di Surabaya ditemukan sebanyak 72 kendaraan yang telah melunasi pajak kendaraan, sedangkan di Bandung hanya terdapat 66 kendaraan saja yang telah melunasi Pajak kendaraan. ujilah perbedaan proporsi kendaraan di dua kota tersebut dengan memakai taraf nyata 0.05
Mapel Matematika, Jenjang Sekolah Menengah Pertama
Sampel sebanyak 100 kendaraan bermotor, ditemukan 72 kendaraan di Surabaya melunasi pajak kendaraan dan ditemukan 66 kendaraan di Bandung melunasi pajak kendaraan. Maka dari uji beda dua proporsi tidak ada perbedaan pada kendaraan di dua kota tersebut.
Penjelasan dengan langkah-langkah
p₁ = 72 : 100 = 0,72
p₂ = 66 : 100 = 0,66
z = Z₀ . √[p₁(1-p₁) : n₁] + [p₂(1-p₂) : n₂]
z = 1,96 x √[0,72(1 – 0,72) : 100] + [0,66(1 – 0,66) : 100]
z = 1,96 x √0,002 + 0,002
z = 1,96 x √0,004
z = 1,96 x 0,0632
z = 0,12
Statistik hitung z = 0,12 < 1,96 (Berada di penerimaan Ho), Ho diterima pada taraf nyata 0,05 → tidak ada perbedaan pada kendaraan di dua kota tersebut.
Uji beda merupakan uji hipotesis yang menentukan ada tidaknya perbedaan yang signifikan antara dua kelompok. Ada berbagai tes yang dapat dilakukan pada rata-rata atau proporsi. Uji beda membandingkan perbedaan proporsi antara dua kelompok. Uji beda proporsi digunakan untuk membandingkan perbedaan antara dua kelompok pada variabel dimana data diperoleh dengan menghitung selisih proporsi masing-masing kelompok.
Uji beda dua proporsi merupakan uji hipotesis untuk mengetahui ada tidaknya perbedaan mean atau proporsi dua kelompok data yang diambil dari dua populasi. Sebuah tes dapat dilakukan untuk melihat apakah perbedaan antara dua proporsi signifikan.
Pelajari lebih lanjut
- Materi tentang uji proporsi
- Materi tentang uji beda dua proporsi
- Materi tentang uji hipotesis
Detail jawaban
Kelas: 11
Mapel: Matematika
Bab: Statistika
Kode: 11.2.7
#AyoBelajar #SPJ2
Pertanyaan Baru di Matematika
135×35:
tulislah kali kali di atas jalan ke bawah
Matematika, Sekolah Menengah Atas
3 1/4 kg – 1.75 kg + 2 1/2 kg = ?
Matematika, Sekolah Menengah Pertama
Jawaban:
3¼ kg – 1,75 kg + 2 ½ kg = 4kg
Penjelasan dengan langkah-langkah:
Jawaban:
4 kg
Penjelasan dengan langkah-langkah:
3 1/4 kg – 1,75 kg + 2 1/2 kg = ?
(Ubah dahulu semuanya menjadi pecahan)
13/4 kg – 175/100 kg + 5/2 kg = ?
(Samakan semua penyebut nya terlebih dahulu)
325/100 – 175/100 + 250/100 =
150/100 + 250/100 = 400/100
= 4 kg
Data berat badan siswa adalah : 53, 25, 32, 32, 31, 35, 25, 25, 27, 53. Banyak siswa yang mempunyai berat badan terendah dan tertinggi adalah
jawab jawab jawab jawab jawab jawab jawab jawab jawab jawab jawab jawab jawab jawab jawab jawab jawab jawab jawab jawab jawab jawab
Matematika, Sekolah Menengah Pertama
25 : 3 siswa
27 : 1 siswa
31 : 1 siswa
32 : 2 siswa
35 : 1 siswa
53 : 2 siswa
Penjelasan dengan langkah-langkah:
data berat badan siswa:
53,25,32,32,31,35,25,25,27,53.
berat badan │banyak siswa
─────────────
53 │2 siswa
25 │3 siswa
32 │2 siswa
31 │1 siswa
35 │1 siswa
27 │1 siswa
─────────────
bb terendah : 25 kg
bb tertinggi : 53 kg
25 kg(terendah) : 3 siswa
53 kg (tertinggi) : 2 siswa
﹋﹋﹋﹋﹋﹋﹋﹋﹋﹋﹋﹋﹋
::maaf kalo salah^^
::jadikan jawaban terbaik ya
Kuis Jelaskan mengapa rumus menghitung luas segitiga adalah ½ x alas x tinggi
Matematika, Sekolah Menengah Pertama
Penjelasan dengan langkah-langkah:
- karena rumus luas segitiga didapatkan dari rumus luas persegi panjang , mengapa?
- karena jika persegi panjang itu dibelah menjadi 2 maka akan menjadi segitiga
- jadi rumus luas persegi panjang adalah p × l
- dan luas segitiga adalah ½ × a × t
koreksi
✨ Penyelesaian Soal ✨
[ Soal ]
Jelaskan mengapa rumus menghitung luas segitiga adalah ½ x alas x tinggi
_________________
☛ Penjelasan Soal
✨ Pengertian
Segitiga adalah Sebuah Bagun Datar Yang Memiliki 3 Sisi + 3 Sudut. Segitiga Terdiri dari Kata “Segi” dan “Tiga” Yang Artinya Memiliki Jumlah segi sebanyak 3.
✨ Rumus
Rumus-rumus Segitiga :
↪ Rumus Luas
Atau :
↪ Rumus Keliling
✨ Penjelasan Mengenai Rumus
1. Keliling
Rumus Keliling Segitiga Adalah a + b + c. Seperti yang Kita Tau, Bahwa Sisi Segitiga Ada 3 Buah. Lalu, Mengapa Rumusnya Bukan a + b + c + d ?
Rumus Keliling Segitiga Bukan a + b + c + d Karena Sisi segitiga Hanya Berjumlah 3 Buah. Maka, Rumusnya adalah [ a + b + c ] Bukan a + b + c + d.
2. Luas
Nah, Ini adalah Penjelasan Berdasarkan Soal. Luas Segitiga adalah ½ × a × t ( atau (( a × t ) ÷ 2 )) Karena Segitiga Merupakan Belahan dari Bangun datar Persegi panjang. ditambah Lagi Segitiga Mempunyai 3 Sisi.
Seperti yang kita Tau, Rumus Luas Persegi Panjang adalah ( p × l ) Dan disini, Adalah rumus ½ Persegi Panjang, Yang kita Sebut Dengan Segitiga. Makanya Rumus mencari Luas segitiga Harus dikalikan ½ atau dibagi 2, Karena Segitiga Merupakan Belahan dari Persegi Panjang.
☛ Kesimpulan
- Maka, Dapat Kita Simpulkan Bahwa Rumus mencari Luas segitiga Harus dikalikan ½ atau dibagi 2, Karena Segitiga Merupakan Belahan dari Persegi Panjang.
☛ Detail jawaban
- Kelas : 4/SD
- Mapel : Matematika
- Materi : Luas dan Keliling Bangun Datar
- Kode soal : 2
- Kode kategorisasi : 4.2.1
- Kata Kunci : Rumus, Segitiga, Luas, ½
Semoga Bisa Bermanfaat-!
#BrainlyMathematic
Soal :
88 × 91
9¹² ÷ 9¹
8!
otw hapus.
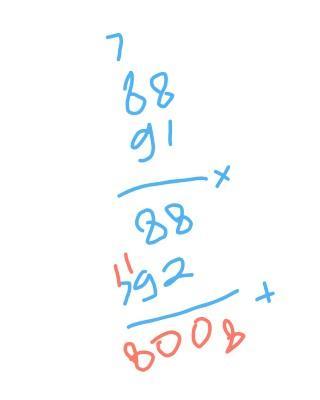
Matematika, Sekolah Menengah Pertama
Jawaban:
Perkalian:
88 × 91
= terlampir
Bentuk AKAR:
Faktorial:
8!
= 8×7×6×5×4×3×2×1
= 56×30×12×2
= 1.680 × 24
= 40.320
Soal 1
88 × 91
= 8.008
—–
Soal 2
—–
Soal 3
8!
= 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 56 × 6 × 5 × 4 × 3 × 2 × 1
= 336 × 5 × 4 × 3 × 2 × 1
= 1.680 × 4 × 3 × 2 × 1
= 6.720 × 3 × 2 × 1
= 20.160 × 2 × 1
= 40.320 × 1
= 40.320
—–
